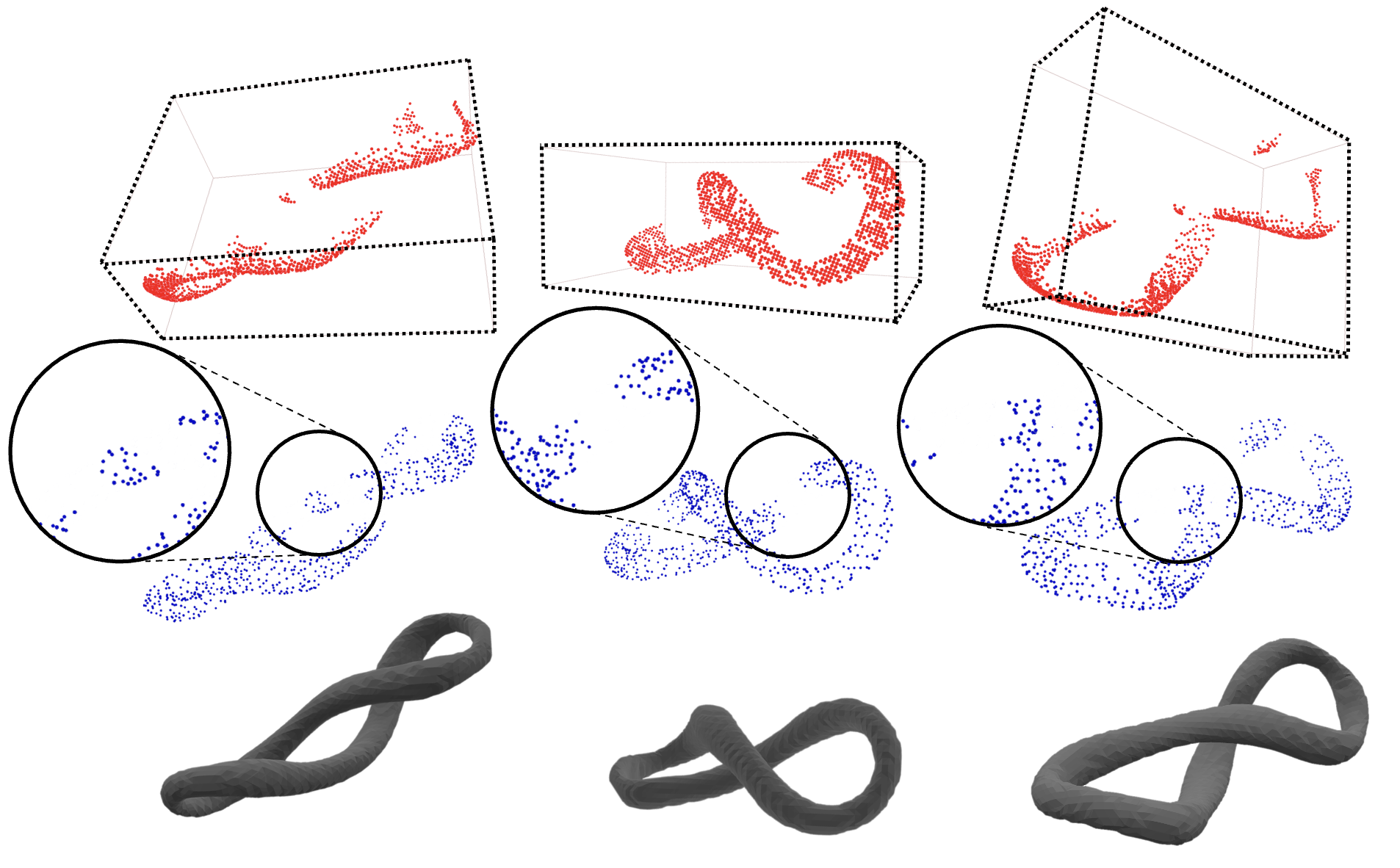
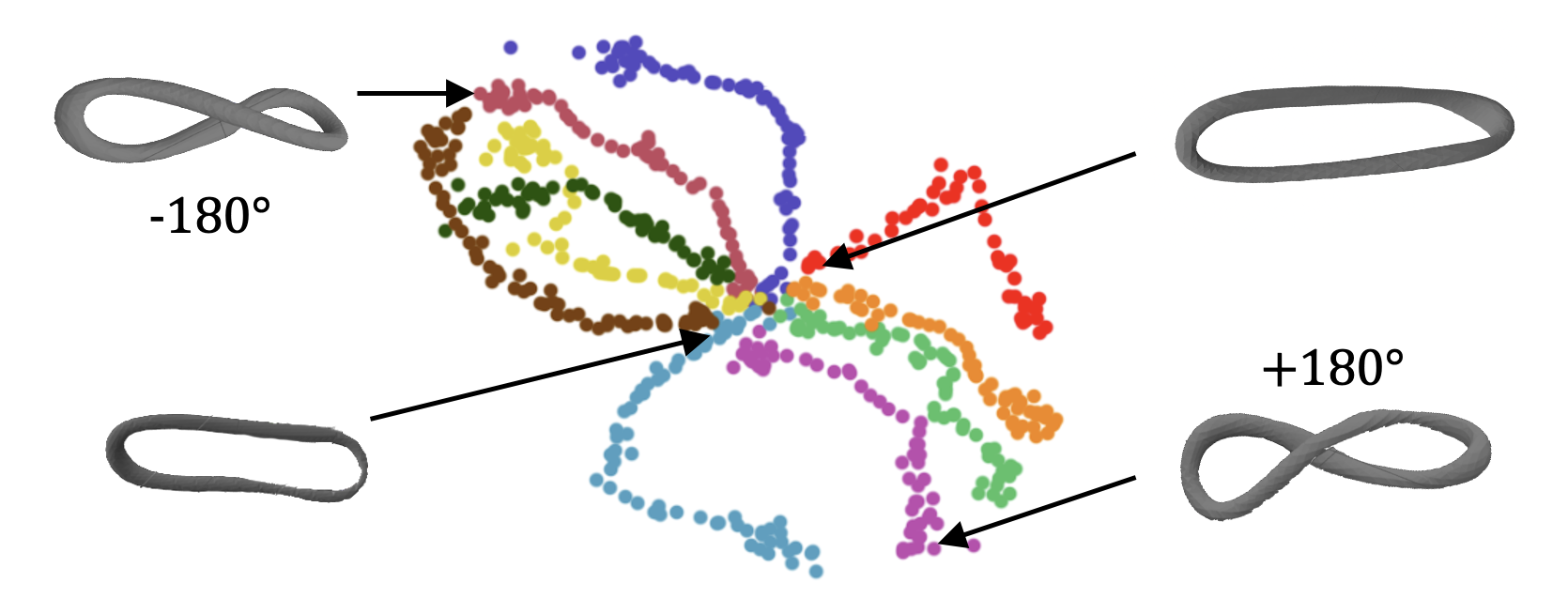
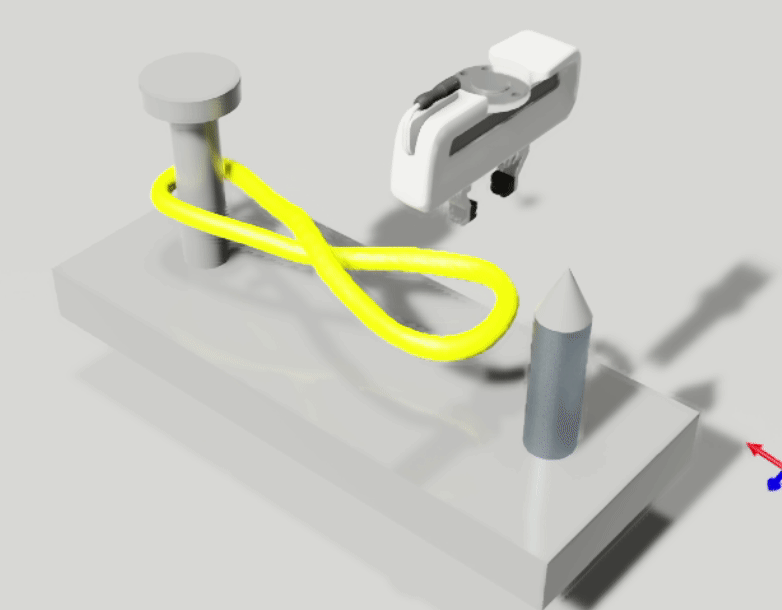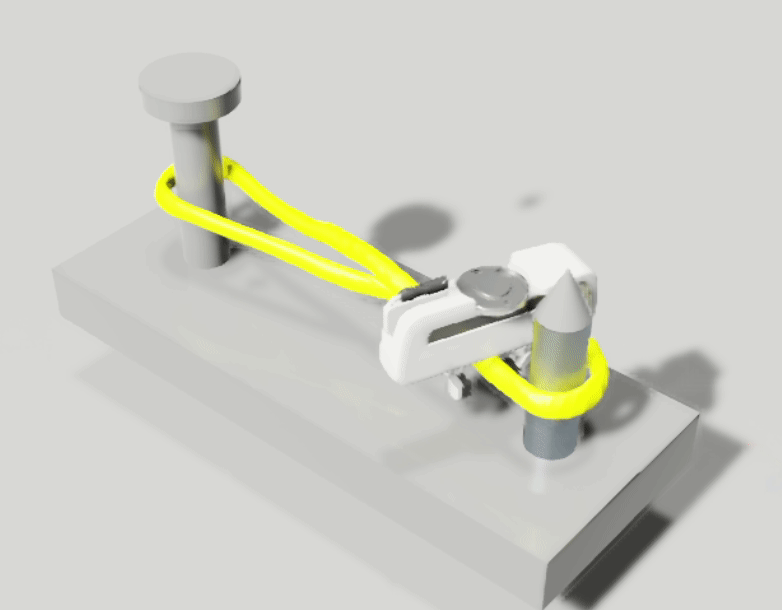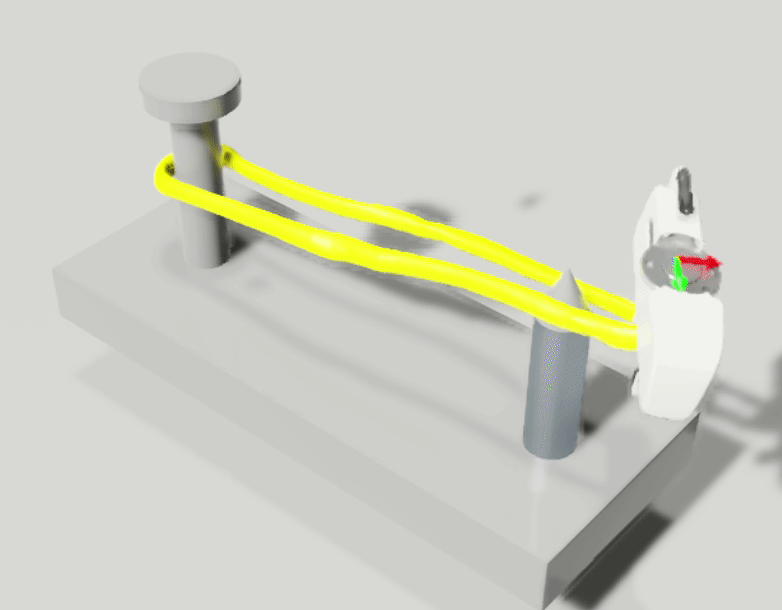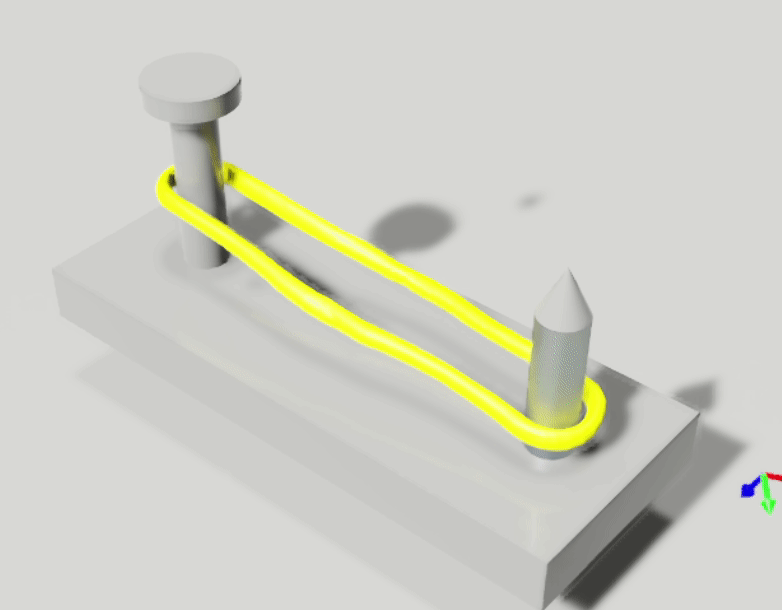
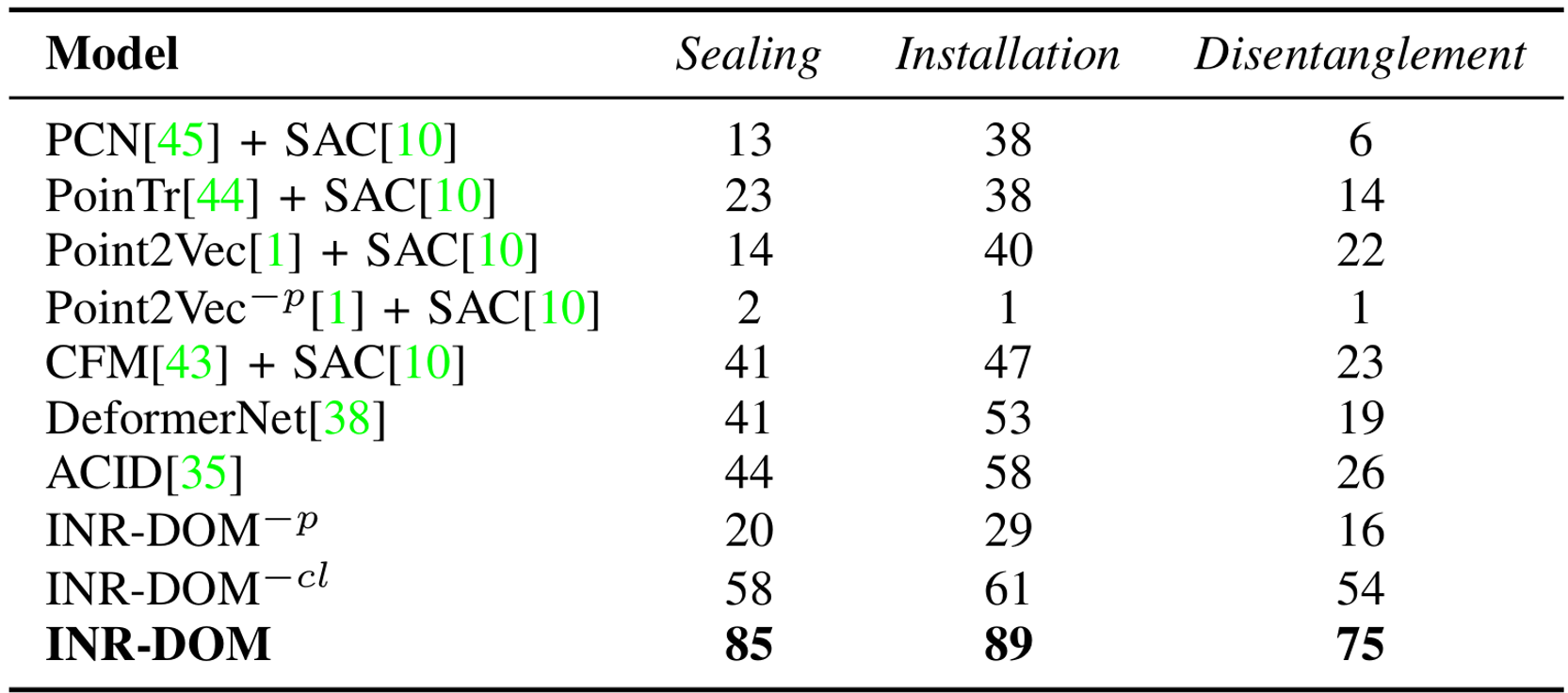
We aim to solve the problem of manipulating deformable objects, particularly elastic bands, in real-world scenarios. However, deformable object manipulation (DOM) requires a policy that works on a large state space due to the unlimited degree of freedom (DoF) of deformable objects. Further, their dense but partial observations (e.g., images or point clouds) may increase the sampling complexity and uncertainty in policy learning. To figure it out, we propose a novel implicit neural-representation (INR) learning for elastic DOMs, called INR-DOM. Our method learns consistent state representations associated with partially observable elastic objects reconstructing a complete and implicit surface represented as a signed distance function. Furthermore, we perform exploratory representation fine-tuning through reinforcement learning (RL) that enables RL algorithms to effectively learn exploitable representations while efficiently obtaining a DOM policy. We perform quantitative and qualitative analyses building three simulated environments and real-world manipulation studies with a Franka Emika Panda arm.